-Un término es una expresión algebraica elemental donde se encuentran solo operaciones de multiplicación y división de números y letras. El número se llama coeficiente y las letras conforman la parte literal. Tanto el número como cada letra pueden estar elevados a una potencia. En una expresión algebraica con varios términos, éstos están separados con signos de suma y resta.
Término independiente
El término independiente es el que consta de solo un valor numérico y no tiene parte literal.Términos semejantes
Los términos semejantes son los que tienen exactamente la misma parte literal (con las mismas letras elevadas a los mismos exponentes), y varían solo en el coeficiente. Solo se pueden sumar y restar términos semejantes. No se pueden sumar y restar términos que no sean semejantes; sin embargo, se puede multiplicar y dividir todo tipo de términos. Si en una expresión algebraica hay varios términos semejantes, éstos se pueden simplificar sumándolos o restándolos.Grado de un término
El grado de un término puede ser de dos tipos: grado absoluto y grado relativo.Polinomio
Un polinomio es una expresión algebraica en la cual solo intervienen las operaciones de suma, resta y multiplicación, así como exponentes enteros positivos.Cuando el polinomio consta de uno, de dos o de tres términos se llama monomio, binomio otrinomio, respectivamente. Generalmente, un polinomio P en la variable x se expresa como:Valor numérico de un polinomio
Es el valor que se obtiene al sustituir las letras por valores numéricos y luego realizar las operaciones del polinomio.Leyes del álgebra elemental
Propiedades de las operaciones
- La operación de adición (+)
- se escribe

- esconmutativa:
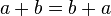
- es asociativa:

- tiene una operación inversa, llamada sustracción :
 , que es igual a sumar un
, que es igual a sumar un - número negativo ,

- tiene un elemento neutro 0 que no altera la suma:

- se escribe
- La operación de multiplicación (×)
- se escribe
 ó
ó 
- es conmutativa:
 =
= 
- es asociativa:

- es abreviada por yuxtaposición:
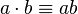
- tiene una operación inversa, para números diferentes a cero, llamada división
 , que es igual a multiplicar por el recíproco,
, que es igual a multiplicar por el recíproco, 
- tiene un elemento neutro 1 que no altera la multiplicación:

- es distributina respecto la adición:

- se escribe
- La operación de potenciación :
- se escribe

- es una multiplicación repetida:
 (n veces)
(n veces) - no es ni comutativa ni asociativa: en general
 y
y 
- tiene una operación inversa, llamada logaritmo:
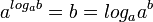
- puede ser escrita en términos de raíz n-ésima:
![\ a^{m/n} \equiv (\sqrt[n]{a^{m}})](http://upload.wikimedia.org/math/9/d/c/9dce189c9cd5c2644b62a96c54e7eb83.png) y por lo tanto las raíces pares de números negativos no existen en el sistema de los números reales. (Ver: sistema de numeros complejos).
y por lo tanto las raíces pares de números negativos no existen en el sistema de los números reales. (Ver: sistema de numeros complejos). - es distributiva con respecto a la multiplicación:

- tiene la propiedad:

- tiene la propiedad:
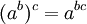
- se escribe
Orden de las operaciones
Para completar el valor de una expresión, es necesario calcular partes de ella en un orden particular, conocido como el orden de prioridad o el orden de precedencia de las operaciones. Primero se calculan los valores de las expresiones encerradas en signos de agrupación (paréntesis, corchetes, llaves), luego las multiplicaciones y divisiones y, por último, las sumas y las restas.Propiedades de la igualdad
La relación deigualdad (=) es:- reflexiba

- sométrica : si
 entonces
entonces 
- transitiva: si
 y
y  entonces
entonces 
Leyes de la igualdad
La relación de igualdad (=) tiene las propiedades siguientes:- si
 y
y  entonces
entonces  y
y 
- si
 entonces
entonces 
- si dos símbolos son iguales, entonces uno puede ser sustituido por el otro.
- regularidad de la suma: trabajando con números reales o complejos sucede que si
 entonces
entonces  .
. - regularidad condicional de la multiplicación: si
 y
y  no es cero, entonces
no es cero, entonces  .
.
Leyes de la desigualdad
La relación de desigualdad (<) tiene las siguientes propiedades:- de transitividad: si
 y
y  entonces
entonces 
- si
 y
y  entonces
entonces 
- si
 y
y  entonces
entonces 
- si
 y
y 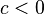 entonces
entonces 


No hay comentarios:
Publicar un comentario